Portal:Mathematics
- አማርኛ
- العربية
- Avañe'ẽ
- Авар
- تۆرکجه
- বাংলা
- 閩南語 / Bân-lâm-gú
- Беларуская (тарашкевіца)
- Bikol Central
- Български
- Català
- Cebuano
- Čeština
- الدارجة
- Deutsch
- Eesti
- Ελληνικά
- Español
- فارسی
- Français
- Gĩkũyũ
- 한국어
- Hausa
- Հայերեն
- हिन्दी
- Bahasa Indonesia
- Interlingua
- Íslenska
- Italiano
- עברית
- ქართული
- Қазақша
- Kiswahili
- Kreyòl ayisyen
- Kurdî
- Latina
- Lietuvių
- Magyar
- Македонски
- Malti
- مصرى
- ဘာသာမန်
- Bahasa Melayu
- မြန်မာဘာသာ
- Nederlands
- 日本語
- Oʻzbekcha / ўзбекча
- ਪੰਜਾਬੀ
- پښتو
- Picard
- Polski
- Português
- Română
- Runa Simi
- Русский
- Shqip
- සිංහල
- سنڌي
- Slovenčina
- Soomaaliga
- کوردی
- Српски / srpski
- Suomi
- Svenska
- தமிழ்
- Taclḥit
- Татарча / tatarça
- ၽႃႇသႃႇတႆး
- ไทย
- Тоҷикӣ
- Türkçe
- Українська
- اردو
- Tiếng Việt
- 文言
- 吴语
- ייִדיש
- Yorùbá
- 粵語
- Zazaki
- 中文
- Batak Mandailing
- ⵜⴰⵎⴰⵣⵉⵖⵜ ⵜⴰⵏⴰⵡⴰⵢⵜ
Tools
Actions
General
Print/export
In other projects
Appearance
Portal maintenance status: (December 2018)
|
Wikipedia portal for content related to Mathematics
-
Abacus, a ancient hand-operated calculating.
-
Portrait of Emmy Noether, around 1900.
Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)
Featured articles – load new batch
-
Image 1
The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.
Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...) -
Image 2

Logic studies valid forms of inference like modus ponens.
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.
Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like(and) or
(if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
-
Image 3

The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group S̃3
The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers (..., −2, −1, 0, 1, 2, ...) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.
A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...) -
Image 4

Plots of logarithm functions, with three commonly used bases. The special points logb b = 1 are indicated by dotted lines, and all curves intersect in logb 1 = 0.
In mathematics, the logarithm to base b is the inverse function of exponentiation with base b. That means that the logarithm of a number x to the base b is the exponent to which b must be raised to produce x. For example, since 1000 = 103, the logarithm baseof 1000 is 3, or log10 (1000) = 3. The logarithm of x to base b is denoted as logb (x), or without parentheses, logb x. When the base is clear from the context or is irrelevant it is sometimes written log x.
The logarithm base 10 is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number e ≈ 2.718 as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base 2 and is frequently used in computer science. (Full article...) -
Image 5One of Molyneux's celestial globes, which is displayed in Middle Temple Library – from the frontispiece of the Hakluyt Society's 1889 reprint of A Learned Treatise of Globes, both Cœlestiall and Terrestriall, one of the English editions of Robert Hues' Latin work Tractatus de Globis (1594)
Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.
Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...) -
Image 6Portrait by August Köhler, c. 1910, after 1627 original
Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ⓘ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.
Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. (Full article...) -
Image 7

Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.
In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history". In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics". (Full article...) -
Image 8In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.
Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...) -
Image 9
Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ⓘ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.
Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...) -
Image 10

Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...) -
Image 11
Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.
Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...) -
Image 12Archimedes Thoughtful by Fetti (1620)
Archimedes of Syracuse (/ˌɑːrkɪˈmiːdiːz/ AR-kim-EE-deez; c. 287 – c. 212 BC) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is considered one of the leading scientists in classical antiquity. Regarded as the greatest mathematician of ancient history, and one of the greatest of all time, Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.
Archimedes' other mathematical achievements include deriving an approximation of pi (π), defining and investigating the Archimedean spiral, and devising a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, working on statics and hydrostatics. Archimedes' achievements in this area include a proof of the law of the lever, the widespread use of the concept of center of gravity, and the enunciation of the law of buoyancy known as Archimedes' principle. He is also credited with designing innovative machines, such as his screw pump, compound pulleys, and defensive war machines to protect his native Syracuse from invasion. (Full article...) -
Image 13

Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.
Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...) -
Image 14Elementary algebra studies which values solve equations formed using arithmetical operations.
Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.
Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...) -
Image 15

The weighing pans of this balance scale contain zero objects, divided into two equal groups.
In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
Good articles – load new batch
-
Image 1
Alan Mathison Turing (/ˈtjʊərɪŋ/; 23 June 1912 – 7 June 1954) was an English mathematician, computer scientist, logician, cryptanalyst, philosopher and theoretical biologist. He was highly influential in the development of theoretical computer science, providing a formalisation of the concepts of algorithm and computation with the Turing machine, which can be considered a model of a general-purpose computer. Turing is widely considered to be the father of theoretical computer science.
Born in London, Turing was raised in southern England. He graduated from King's College, Cambridge, and in 1938, earned a doctorate degree from Princeton University. During World War II, Turing worked for the Government Code and Cypher School at Bletchley Park, Britain's codebreaking centre that produced Ultra intelligence. He led Hut 8, the section responsible for German naval cryptanalysis. Turing devised techniques for speeding the breaking of German ciphers, including improvements to the pre-war Polish bomba method, an electromechanical machine that could find settings for the Enigma machine. He played a crucial role in cracking intercepted messages that enabled the Allies to defeat the Axis powers in many engagements, including the Battle of the Atlantic. (Full article...) -
Image 2

Partition of a directed graph into a minimum feedback arc set (red dashed edges) and a maximum acyclic subgraph (blue solid edges)
In graph theory and graph algorithms, a feedback arc set or feedback edge set in a directed graph is a subset of the edges of the graph that contains at least one edge out of every cycle in the graph. Removing these edges from the graph breaks all of the cycles, producing an acyclic subgraph of the given graph, often called a directed acyclic graph. A feedback arc set with the fewest possible edges is a minimum feedback arc set and its removal leaves a maximum acyclic subgraph; weighted versions of these optimization problems are also used. If a feedback arc set is minimal, meaning that removing any edge from it produces a subset that is not a feedback arc set, then it has an additional property: reversing all of its edges, rather than removing them, produces a directed acyclic graph.
Feedback arc sets have applications in circuit analysis, chemical engineering, deadlock resolution, ranked voting, ranking competitors in sporting events, mathematical psychology, ethology, and graph drawing. Finding minimum feedback arc sets and maximum acyclic subgraphs is NP-hard; it can be solved exactly in exponential time, or in fixed-parameter tractable time. In polynomial time, the minimum feedback arc set can be approximated to within a polylogarithmic approximation ratio, and maximum acyclic subgraphs can be approximated to within a constant factor. Both are hard to approximate closer than some constant factor, an inapproximability result that can be strengthened under the unique games conjecture. For tournament graphs, the minimum feedback arc set can be approximated more accurately, and for planar graphs both problems can be solved exactly in polynomial time. (Full article...) -
Image 3
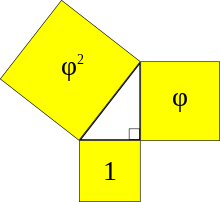
A Kepler triangle is a right triangle formed by three squares with areas in geometric progression according to the golden ratio.
A Kepler triangle is a special right triangle with edge lengths in geometric progression. The ratio of the progression iswhere
is the golden ratio, and the progression can be written:
, or approximately
. Squares on the edges of this triangle have areas in another geometric progression,
. Alternative definitions of the same triangle characterize it in terms of the three Pythagorean means of two numbers, or via the inradius of isosceles triangles.
This triangle is named after Johannes Kepler, but can be found in earlier sources. Although some sources claim that ancient Egyptian pyramids had proportions based on a Kepler triangle, most scholars believe that the golden ratio was not known to Egyptian mathematics and architecture. (Full article...) -
Image 4

Thoralf Skolem, after whom the paradox is named
In mathematical logic and philosophy, Skolem's paradox is the apparent contradiction that a countable model of first-order set theory could contain an uncountable set. The paradox arises from part of the Löwenheim–Skolem theorem; Thoralf Skolem was the first to discuss the seemingly contradictory aspects of the theorem, and to discover the relativity of set-theoretic notions now known as non-absoluteness. Although it is not an actual antinomy like Russell's paradox, the result is typically called a paradox and was described as a "paradoxical state of affairs" by Skolem.
In model theory, a model corresponds to a specific interpretation of a formal language or theory. It consists of a domain (a set of objects) and an interpretation of the symbols and formulas in the language, such that the axioms of the theory are satisfied within this structure. The Löwenheim–Skolem theorem shows that any model of set theory in first-order logic, if it is consistent, has an equivalent model that is countable. This appears contradictory, because Georg Cantor proved that there exist sets which are not countable. Thus the seeming contradiction is that a model that is itself countable, and which therefore contains only countable sets, satisfies the first-order sentence that intuitively states "there are uncountable sets". (Full article...) -
Image 5Sunday Osarumwense Iyahen (3 October 1937 – 28 January 2018) was a Nigerian mathematician and politician, recognised for his contributions to the field of topological vector spaces and his service as a senator representing Bendel Central Senatorial District. Born in Benin City, Edo State, Nigeria, Iyahen was the eldest of at least seventeen children and embarked on an academic journey that led him to earn a first-class honours degree in mathematics from the University of Ibadan and later a Ph.D. and D.Sc. from the University of Keele.
Iyahen's academic career was marked by his tenure as a professor of mathematics at several universities in Nigeria and abroad. He served as the Head of the Department of Mathematics and Dean of the Faculty of Science at the University of Ibadan before joining the Institute of Technology, Benin (now known as the University of Benin), where he became the founding dean of the Faculty of Physical Sciences. His scholarly work includes over 100 published papers and contributions as editor-in-chief for mathematical journals. He was honoured with fellowships from the Nigerian Academy of Science and the Mathematical Association of Nigeria. As a politician, he was elected as a senator, where he contributed to national policy and development. (Full article...) -
Image 6In mathematics and computer science, the BIT predicate, sometimes written
, is a predicate that tests whether the
th bit of the number
(starting from the least significant digit) is 1, when
is written as a binary number. Its mathematical applications include modeling the membership relation of hereditarily finite sets, and defining the adjacency relation of the Rado graph. In computer science, it is used for efficient representations of set data structures using bit vectors, in defining the private information retrieval problem from communication complexity, and in descriptive complexity theory to formulate logical descriptions of complexity classes. (Full article...)
-
Image 7

A double bubble. Note that the surface separating the small lower bubble from the large bubble bulges into the large bubble.
In the mathematical theory of minimal surfaces, the double bubble theorem states that the shape that encloses and separates two given volumes and has the minimum possible surface area is a standard double bubble: three spherical surfaces meeting at angles of 120° on a common circle. The double bubble theorem was formulated and thought to be true in the 19th century, and became a "serious focus of research" by 1989, but was not proven until 2002.
The proof combines multiple ingredients. Compactness of rectifiable currents (a generalized definition of surfaces) shows that a solution exists. A symmetry argument proves that the solution must be a surface of revolution, and it can be further restricted to having a bounded number of smooth pieces. Jean Taylor's proof of Plateau's laws describes how these pieces must be shaped and connected to each other, and a final case analysis shows that, among surfaces of revolution connected in this way, only the standard double bubble has locally-minimal area. (Full article...) -
Image 8

Pell's equation for n = 2 and six of its integer solutions
Pell's equation, also called the Pell–Fermat equation, is any Diophantine equation of the formwhere n is a given positive nonsquare integer, and integer solutions are sought for x and y. In Cartesian coordinates, the equation is represented by a hyperbola; solutions occur wherever the curve passes through a point whose x and y coordinates are both integers, such as the trivial solution with x = 1 and y = 0. Joseph Louis Lagrange proved that, as long as n is not a perfect square, Pell's equation has infinitely many distinct integer solutions. These solutions may be used to accurately approximate the square root of n by rational numbers of the form x/y.
This equation was first studied extensively in India starting with Brahmagupta, who found an integer solution toin his Brāhmasphuṭasiddhānta circa 628. Bhaskara II in the 12th century and Narayana Pandit in the 14th century both found general solutions to Pell's equation and other quadratic indeterminate equations. Bhaskara II is generally credited with developing the chakravala method, building on the work of Jayadeva and Brahmagupta. Solutions to specific examples of Pell's equation, such as the Pell numbers arising from the equation with n = 2, had been known for much longer, since the time of Pythagoras in Greece and a similar date in India. William Brouncker was the first European to solve Pell's equation. The name of Pell's equation arose from Leonhard Euler mistakenly attributing Brouncker's solution of the equation to John Pell. (Full article...)
-
Image 9

Fibonacci nim is played with a pile of coins. The number of coins in this pile, 21, is a Fibonacci number, so a game starting with this pile and played optimally will be won by the second player.
Fibonacci nim is a mathematical subtraction game, a variant of the game of nim. Players alternate removing coins from a pile, on each move taking at most twice as many coins as the previous move, and winning by taking the last coin. The Fibonacci numbers feature heavily in its analysis; in particular, the first player can win if and only if the starting number of coins is not a Fibonacci number. A complete strategy is known for best play in games with a single pile of counters, but not for variants of the game with multiple piles. (Full article...) -
Image 10

Walton in Pomona College's Walker Lounge c. 1957
Jean Brosius Walton (March 6, 1914 – July 5, 2006) was an American academic administrator and women's studies scholar. She spent the bulk of her career at Pomona College in Claremont, California.
Born to a Pennsylvania Quaker family, Walton grew up at George School and studied mathematics at Swarthmore College, Brown University and the University of Pennsylvania. She joined Pomona College in 1949 as the Dean of Women, and was promoted to dean of students in 1969 and vice president for student affairs in 1976, three years before her formal retirement. During her tenure, she advocated for women's education, engaged with student protests against the Vietnam War, oversaw reform of residential life policies to eliminate parietal rules, and co-founded the Claremont Colleges' Intercollegiate Women's Studies Program. She earned widespread recognition for her work and was praised by colleagues for her independent and dignified personality. (Full article...) -
Image 11In mathematics, particularly algebraic topology and homology theory, the Mayer–Vietoris sequence is an algebraic tool to help compute algebraic invariants of topological spaces. The result is due to two Austrian mathematicians, Walther Mayer and Leopold Vietoris. The method consists of splitting a space into subspaces, for which the homology or cohomology groups may be easier to compute. The sequence relates the (co)homology groups of the space to the (co)homology groups of the subspaces. It is a natural long exact sequence, whose entries are the (co)homology groups of the whole space, the direct sum of the (co)homology groups of the subspaces, and the (co)homology groups of the intersection of the subspaces.
The Mayer–Vietoris sequence holds for a variety of cohomology and homology theories, including simplicial homology and singular cohomology. In general, the sequence holds for those theories satisfying the Eilenberg–Steenrod axioms, and it has variations for both reduced and relative (co)homology. Because the (co)homology of most spaces cannot be computed directly from their definitions, one uses tools such as the Mayer–Vietoris sequence in the hope of obtaining partial information. Many spaces encountered in topology are constructed by piecing together very simple patches. Carefully choosing the two covering subspaces so that, together with their intersection, they have simpler (co)homology than that of the whole space may allow a complete deduction of the (co)homology of the space. In that respect, the Mayer–Vietoris sequence is analogous to the Seifert–van Kampen theorem for the fundamental group, and a precise relation exists for homology of dimension one. (Full article...) -
Image 12

Selected witch of Agnesi curves (green), and the circles they are constructed from (blue), with radius parameters ,
,
, and
.
In mathematics, the witch of Agnesi (Italian pronunciation: [aɲˈɲeːzi, -eːsi; -ɛːzi]) is a cubic plane curve defined from two diametrically opposite points of a circle.
The curve was studied as early as 1653 by Pierre de Fermat, in 1703 by Guido Grandi, and by Isaac Newton. It gets its name from Italian mathematician Maria Gaetana Agnesi who published it in 1748. The Italian name la versiera di Agnesi is based on Latin versoria (sheet of sailing ships) and the sinus versus.
This was read by John Colson as l’avversiera di Agnesi, where avversiera is translated as "woman who is against God" and interpreted as "witch". (Full article...)
Did you know (auto-generated) – load new batch

- ... that Green Day's "Wake Me Up When September Ends" became closely associated with the aftermath of Hurricane Katrina?
- ... that subgroup distortion theory, introduced by Misha Gromov in 1993, can help encode text?
- ... that despite a mathematical model deeming the ice cream bar flavour Goody Goody Gum Drops impossible, it was still created?
- ... that mathematician Daniel Larsen was the youngest contributor to the New York Times crossword puzzle?
- ... that circle packings in the form of a Doyle spiral were used to model plant growth long before their mathematical investigation by Doyle?
- ... that multiple mathematics competitions have made use of Sophie Germain's identity?
- ... that Ewa Ligocka cooked another mathematician's goose?
- ... that the discovery of Descartes' theorem in geometry came from a too-difficult mathematics problem posed to a princess?
More did you know – view different entries

- … that every positive integer can be written as the sum of three palindromic numbers in every number system with base 5 or greater?
- … that the best known lower bound for the length of the smallest superpermutation was first posted anonymously to the internet imageboard 4chan?
- ...that the mathematician Grigori Perelman was offered a Fields Medal in 2006, in part for his proof of the Poincaré conjecture, which he declined?
- ...that a regular heptagon is the regular polygon with the fewest sides which is not constructible with a compass and straightedge?
- ...that the regular trigonometric functions and the hyperbolic trigonometric functions can be related without using complex numbers through the Gudermannian function?
- ...that the Catalan numbers solve a number of problems in combinatorics such as the number of ways to completely parenthesize an algebraic expression with n+1 factors?
- ...that a ball can be cut up and reassembled into two balls, each the same size as the original (Banach-Tarski paradox)?
Showing 7 items out of 75
Featured pictures
-
Image 2Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 4Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 5Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 6Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
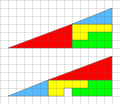
Image 8Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 9Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
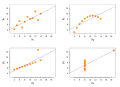
Image 10Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 11Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 12Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 13Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 14Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 15Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 16Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 17Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 18Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 19Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 22Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 23Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 24Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 26Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 27Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 28Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 29Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 30Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 31Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
-
Image 32Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Get involved
- For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.
Categories
Topics
Index of articles
| ARTICLE INDEX: | |
| MATHEMATICIANS: |
Vital articles
- » subpages: Level 4 Mathematics articles, Level 5 Mathematics articles
Discover Wikipedia using portals
Hidden categories:
- Pages using the Phonos extension
- Pages with German IPA
- Pages including recorded pronunciations
- Pages with Polish IPA
- Pages with French IPA
- Pages with Italian IPA
- Wikipedia semi-protected portals
- Manually maintained portal pages from December 2018
- All manually maintained portal pages
- Portals with triaged subpages from December 2018
- All portals with triaged subpages
- Portals with named maintainer
- Wikipedia move-protected portals
- Automated article-slideshow portals with 31–40 articles in article list
- Automated article-slideshow portals with 101–200 articles in article list
- Random portal component with over 50 available subpages